Écouter cet épisode aussi sur :
Résumé
Cette fiche explique l’application de l’optimisation combinatoire et des solveurs pour les sociétés de gestion de fonds. Il met en lumière comment ces techniques de mathématiques appliquées peuvent aider à résoudre des problèmes complexes comme l’allocation de portefeuille ou la planification, en passant de décisions intuitives à des décisions optimisées, traçables et rapides. La fiche présente les concepts fondamentaux de l’optimisation sous contraintes, incluant la fonction objectif, les contraintes et les variables de décision, et propose des outils comme Excel Solver. Enfin, elle offre des exemples concrets, des avantages et des conseils pratiques pour démarrer l’implémentation de ces méthodes
NB : le podcast de BODIC est généré par l’outil d’IA NotebookLM à partir du contenu de cette fiche PDF écrite par l’équipe Bodic
Introduction
Pourquoi parler d’optimisation combinatoire ?
Dans une société de gestion, de nombreuses décisions sont combinatoires :
● Allocation de portefeuille,
● Planification de comités,
● Sélection de dossiers d’investissement à analyser…
Ces problèmes comportent des contraintes et des objectifs multiples à optimiser.
Les solveurs permettent de passer de l’intuition à la décision optimisée, traçable et rapide.
Ces approches de mathématiques appliquées, déjà utilisées par EDF, SNCF, Air France ou Bouygues pour planifier au mieux leurs ressources, s’appliquent pleinement au quotidien d’un fonds.
Les concepts de base de l’optimisation sous contraintes
- Fonction objectif : ce qu’on cherche à maximiser (ex : rendement) ou à minimiser (ex : risque)
- Contraintes : les frontières du problème à respecter (ex : budget, concentration sectorielle, échéances)
- Variables de décision : elles sont souvent binaires (ex : on sélectionne ou non une cible)
Des outils existent pour modéliser et résoudre ces problèmes :
- Solveurs exacts : Excel Solver, GLPK, Google OR Tool, Gurobi, IBM CPLEX, Hexaly
- Heuristiques : Recherche tabou, algos génétiques…
Exemple concret : Optimisation d’un portefeuille
Problème :
Un fonds doit sélectionner 6 entreprises sur une shortlist de 30 pour composer son portefeuille dans les 2 prochaines années
Objectif :
Maximiser le score composite (croissance + impact + digital)
Contraintes :
● Budget global ≤ 200 M€
● Au moins 3 entreprises du secteur santé
● Pas plus de 2 participations en zone UK
Modélisation sous Excel Solver :
● Variables : 30 cases = 0 ou 1 (choisi ou non)
● Contraintes : budget total, listes des secteurs et des zones
● Objectif : somme pondérée des scores dans une case
Résultat :
Sélection optimale en 1 seconde des 6 entreprises, solution visualisable et ajustable
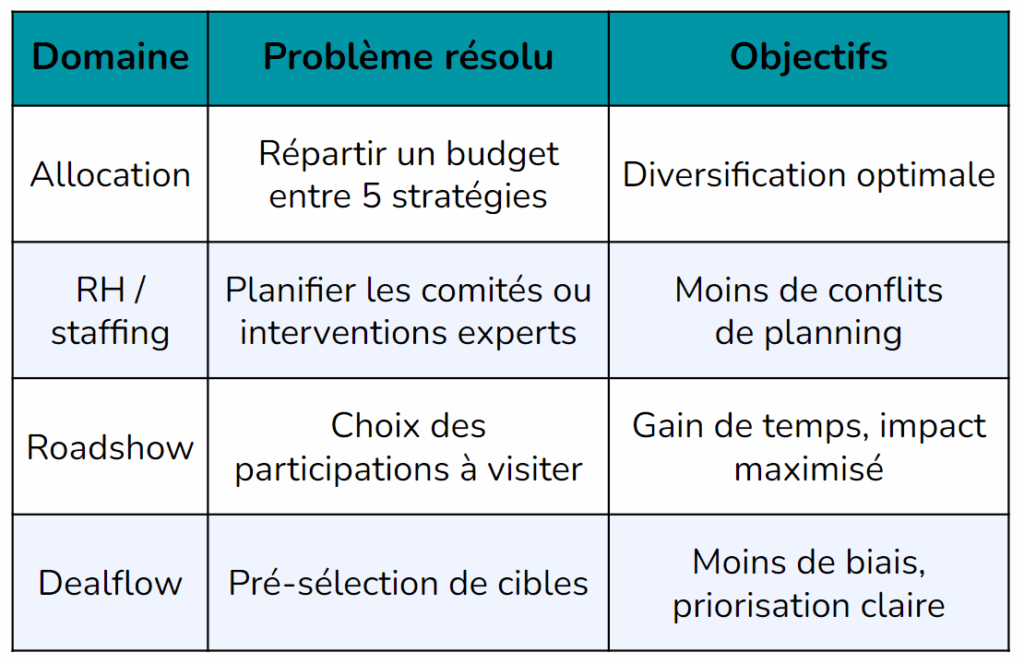
Autres cas d’usage dans une société de gestion
Avantages d’une approche utilisant les mathématiques appliquées
Nos conseils pour démarrer
● Choisissez un problème concret et douloureux à modéliser
● Formulez bien votre objectif : pas trop vague, pas trop complexe. Faites un modèle simple, puis complexifiez ensuite.
● Commencez par Excel Solver avant de basculer sur Python + Hexaly (solveur souverain FR) ou GLPK (solveur opensource)
● Impliquez les utilisateurs métier pour valider les contraintes
● Documentez et conservez les versions de vos modèles
Conclusion
Vous souhaitez aller plus loin ?
BODIC vous accompagne pour mettre en place une démarche IA/Data efficace et souveraine, tout en aidant vos équipes à monter en compétences.
📩 Contactez-nous dès aujourd’hui : contact@bodic.eu